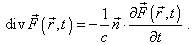Уважаемые коллеги, этой темой я хотел бы, с вашего позволения, открыть обсуждение ряда вопросов развития существующих представлений теории Максвелла, как они видятся с точки зрения классической физики.
Начать хочу с анализа самой простой, скажем, даже тривиальной схемы. Пусть имеется некоторое однородное пространство без зарядов, токов и материальных тел. Пусть в этом пространстве распространяется некоторое динамическое поле, Е-вектор которого направлен вдоль направления распространения волны. Об условиях излучения подобной волны пока не говорим, хотя если кто-то скрупулёзен, можно представить следующую очень упрощённую модель подобного, правда, центрального излучателя:
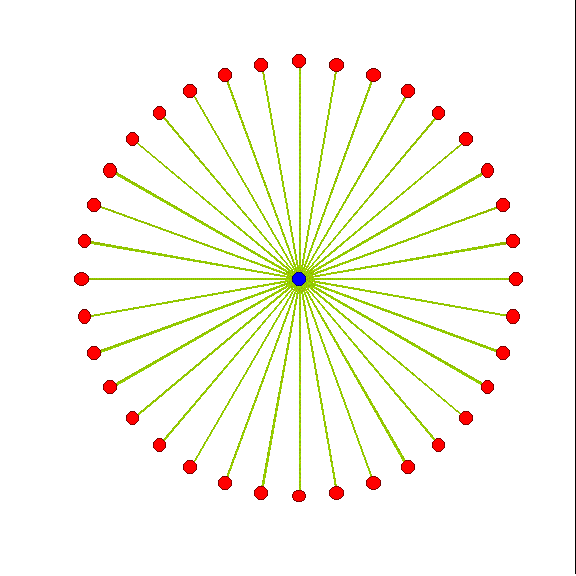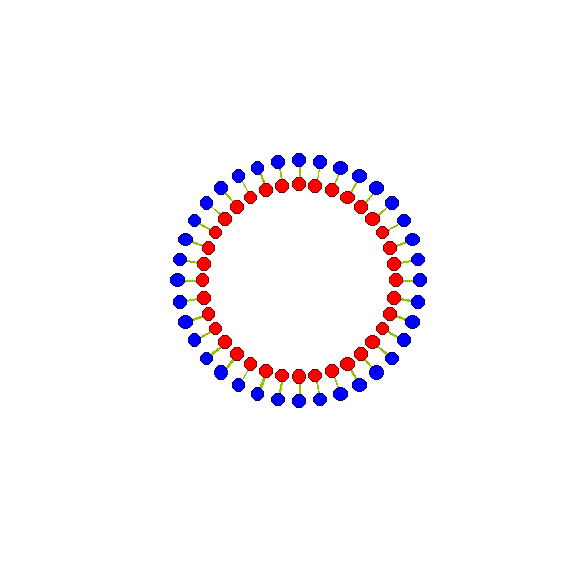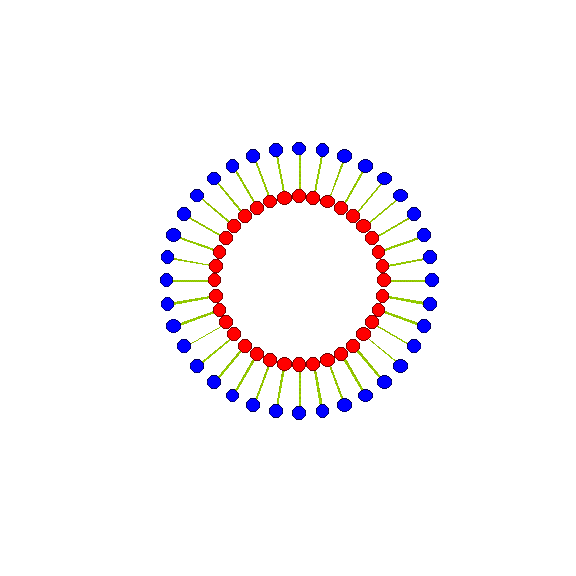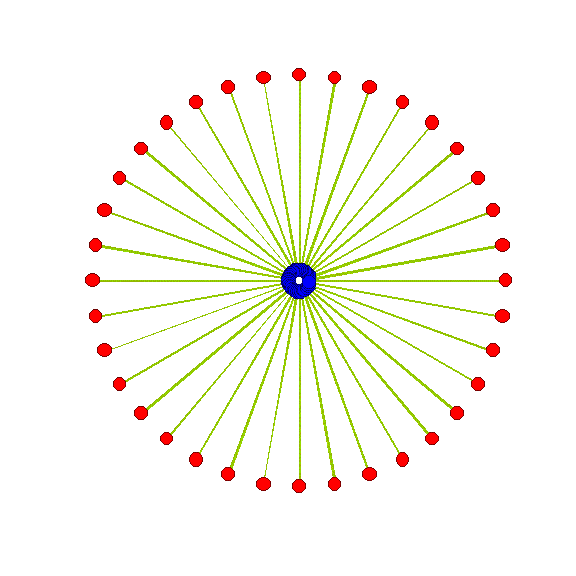
Красным на модели обозначены положительные заряды, а синим – отрицательные. Если размах колебаний будет в половину длины волны, то в целом такой мастодонт будет излучать сферическую продольную волну. Реальные схемы, конечно, иные, но для самого хфакту возможности излучения – вполне достаточно.
Так вот. Рассмотрим поток вектора через некоторый выделенный объём в рассматриваемом одномерном потоке F(x,t) согласно диаграмме, представленной на рисунке ниже:
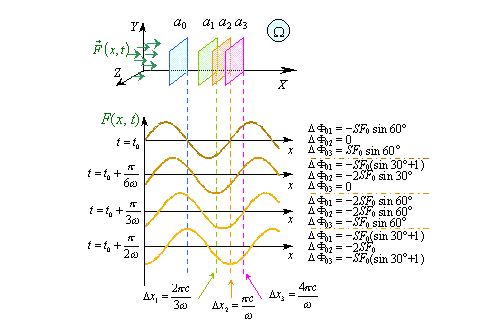
Диаграмма временной зависимости для исследования потока вектора через выделенный объем
Будет ли этот поток вектора для динамического поля обращаться в ноль, как того требуют уравнения Максвелла? У кого какое мнение?